MASONIC GEOMETRY – A KEY TO MOUND BUILDER REMAINS
John G. Keplinger
In studying the remains of the ancient peoples whom we speak of as the Mound Builders we cannot help but be amazed at the remarkable geometrical designs they evolved in stone, in copper and in their earthworks.
Archaeologists know nothing of the meaning of these forms and there are some who even deny that the prehistoric dwellers of the Middle West knew anything of mathematical or geometrical science. The position, however, of the most advanced students is ably set forth in “The Stone Age In America,” by its author, Prof. Warren K. Moorehead, who writes:
“When we realize the point of view, the mind, and the concept of the stone-age man fully, we shall, quite likely, under stand the true import of the strange problematical polished stones so common in the Mississippi Valley. These stand for more than mere ornaments. The very name “ceremonial,” which was afterward changed by that able archaeologist, Professor Holmes, to “problematical,” is a confession of ignorance. These problematical forms are found in Wisconsin, West Virginia, New England, Louisiana, Ohio and Arkansas, and although varying through a multitude of shapes, yet apparently convey substantially the same idea. To the people who lived entirely in the stone-age times, these must have represented certain “sacred mysteries” unknown to white men and the later Indians.
If we compare these objects as Professor Moorehead sug gests we are amazed to find that while they vary through a multitude of shapes they do convey the same idea and that idea is the squaring of the circle as to perimeter and area—a principle which lies at the foundation of the “sacred mysteries,” not only of the Mound Builders but of all the ancient civilizations of the Orient.
To demonstrate this proposition we must refer to the Ma sonic writing of Frank C. Higgins, 320 A. A. S. R.,—without a doubt the ablest and most profound student and writer the Craft has produced since the days of Mackey and Pike.
In his brochure, “The Apron,” Higgins shows that the ancient Oriental priesthoods expressed the squarings of the circle by two basic triangles—one having a base of five and two sides of four parts while the other had a base of four parts and two sides of three each as will be seen upon reference to figures 1 and 2.
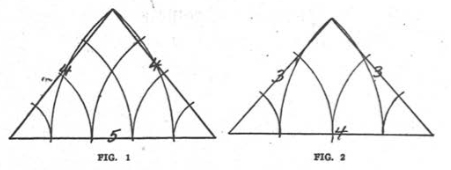
The first figure, Higgins shows, is precisely that of the vertical section of the Great Pyramid of Gizeh. The altitude of this triangle is the radius of a circle whose perimeter is equal to the square drawn on the triangle’s base as will be seen in figure 3 shown on page 246 of the April Azoth . Another significant feature about this triangle is that its altitude and base lines form the Tau cross—the geometrical figure which represents the name Jehovah.
The altitude of the second figure is the radius of a circle whose area is equal to the square drawn on the base of the triangle.
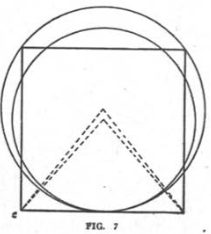
Now let us draw the two circles with a common center. ‘The result is shown in figure 3. Divide the diameter of the larger circles into ten parts. From Us extremities lay off lines tangent to the inner circle. Mark off five parts on each of these lines as indicated and connect the extremities and we will find that the connecting line is also tangent to the inner circle and, if measured, will be found to be equal to six parts exactly.
This is most significant for we find that we thus have 10 plus 5 plus ‘6 plus 5 or 26, which Higgins has shown us in a number of places, is the numerical value of the name Jehovah. If, now, we continue the lines drawn upward from the extremities of the diameter until they intersect we will find that the angle at the point of intersection measures exactly 47 degrees. The significance of this angle is easily perceived if we will but consider that one end of the diameter represents the position of the earth in summer while the other its position in winter. As the earth’s axis inclines 23l/z degrees to the pole of the ecliptic the angle de scribed by the earth’s axis from the two positions is exactly 47 degrees. That the Mound Builders knew of this inclination of the earth’s axis is evident from the gigantic earthwork forms of men which they have left behind them. One of these mounds is illustrated in Switzler’s History of Missouri and shows the legs of the figure open at an angle of precisely 47 degrees and with a representation of the sun between the feet. This, how ever, is not the only evidence that the Mound Builders were adepts in geometrical science. There is much of it. In “Pre historic Times” Lord Avebury states that Circleville, Ohio, obtained its name from a large mound in the shape of a circle which at one time occupied the site of that city. The diameter of the circle was a little over 1000 feet. Besides this circle was a square—each side of which measured about 900 feet. A little calculation will show that this circle and the square beside it were equal in area. In “Atlantis” also, Ignatius Donnelly in forms us that at Hopetown, Ohio, there “are two walled figures— one a square, the other a circle—each containing precisely twenty acres.” Donnelly was so impressed by the remarkable agreement in area of these two figures that he writes of their builders— “they must have possessed regular scales of measurement, and the means of determining angles and of computing the area to be enclosed by the square and the circle so that the space en closed might exactly correspond.”
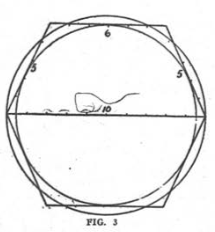
On page 389 of Moorehead’s volume 1, “The Stone Age In North America,” he illustrates an object found on the chest of a skeleton in a gravel pit in Mercer County, Ohio. The original which is in the collection of the Phillips Academy, at Andover, Mass., is made of cannel coal and measures about nine inches. See figure 5. By taking the two holes as centers and following the arcs we get two circles which cut each other at I and J. If, then, we connect these points with the middle of each original arc we have two triangles I A J and I B J which are precisely the same as that of the vertical section of the Great Pyramid, and which gives us the squaring of the circle as to perimeter. Now, if we connect the points C D E F with the center of the figure we get two triangles which are precisely the same as the 3-4-3 triangle shown in figure 2 and which gives us the squaring of the circle as to area.
That the finding of these basic triangles in this figure is not a mere coincidence is proved by the fact that they are found in many forms ranging from the very simple to those which are very complex as will be seen in figures 6 and 7.
If we will turn to page 218, volume II, of Moorehead’s work we will find a plate illustrating a number of copper crescents which are in the collection of the Wisconsin Archaelogical Society. Two of these copper forms are of particular interest and are marked F and E on the original plate. As each yields circles of equal perimeter and equal area we will use F— the better preserved of the two—for our demonstration.
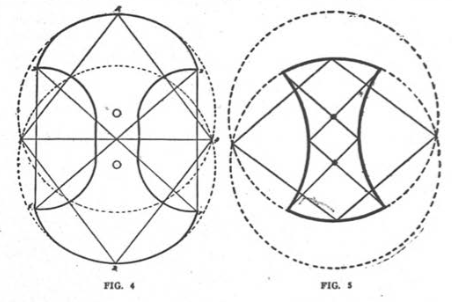
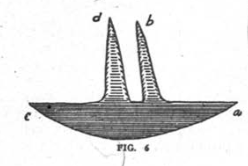
See figure 6. The distance between the points a and b is the radius of a circle whose perimeter is equal to a square drawn on the base c—a. The distance between c and d is the radius of a circle whose area is equal to that of the same square. If, now, we connect the centers of these two circles with the two lower corners of the completed square— figure 7 we will find that one of the triangles has a base of five parts and two sides of four each and that the other has a base of four parts and two sides of three each —thereby conclusively demonstrating that the copper crescents in the collection of the Wisconsin Archaeological Society, as well as many other so-called crescents found in Wisconsin and adjacent states, are the mares and compass of the ancient Mound Builders—a people whose leaders were familiar with the geometrical science of peoples of antiquity whether living in Yucatan, Chaldea, Egypt or lndia.
